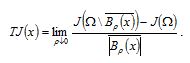The idea of topological derivative is to gain the sensitivity of the objective functional with respect to a point in the design space by introducing a hole and thus directly changing the topology class. The information about how sensitive the objective functional is to the introduction of a hole at a point can be used to evaluate all points in the design space (Figure 1).
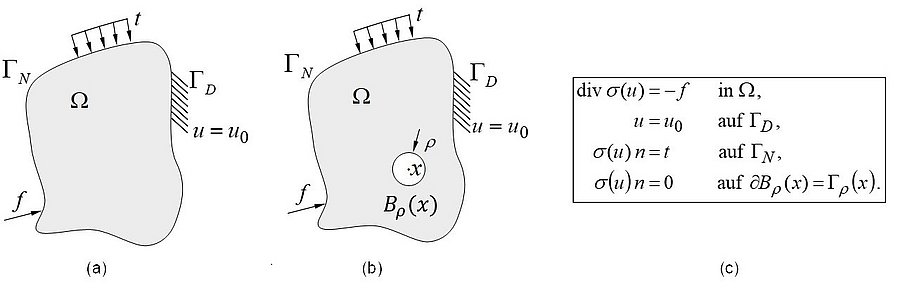
Figure 1: Mechanical problem on the whole body, b) mechanical body with hole, c) equilibrium conditions.
For the optimization problem based on the functional J(Ω) and the mechanical equilibrium conditions, the topological derivative can be determined. For this purpose, a void in the form of a hollow sphere, denoted here as Bρ(x), with radius ρ is inserted into the design space at the point x (cf. Figs. Thus, the difference quotient can be written as
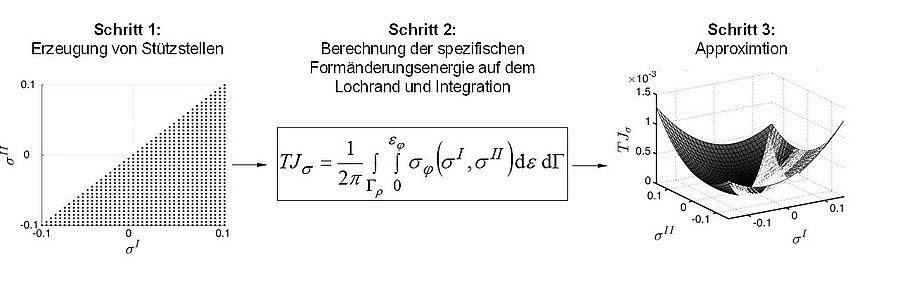
Figure 2: Numerical approach to create an approximation surface for the topological derivative.
The method is established for linear tasks, but for highly non-linear tasks there are currently no usable solutions. This is the starting point of the DFG project "Topological derivatives for topology optimization of crash loaded structures". The topological derivatives are determined numerically and integrated with analytical functions in the optimization process of crash structures. Figure 2 shows a numerical approach to create an approximation surface for the topological derivative.
Weider, K., Schumacher, A. (2018): "Efficient analysis of topological sensitivities for crash problems using LS-Dyna implicit" appears in the Proceedings of the LS-DYNA Forum 2018, 15.-17.10.2018 in Bamberg
Weider, K., Schumacher, A. (2018): "Adjoint method for Topological Derivatives for optimization tasks with material and geometrical nonlinearities" appears in the Proceedings of the 6th International Conference on Engineering Optimization (EngOpt2018), 17-19 September 2018, Lisboa, Portugal
Weider, K., Schumacher, A. (2018): "A topology optimization scheme for crash loaded structures using Topological Derivatives", in: Schumacher, A., Vietor, T., Fiebig, S., Bletzinger, K.-U., Maute, K. (Hrsg.): Advances in Structural and Multidisciplinary Optimization, Proceedings of the 12th World Congress of Structural and Multidisciplinary Optimization (WCSMO12), Springer Nature, 1601-1614, 2018
Weider, K., Schumacher, A. (2016): “On the calculation of Topological Derivatives considering an exemplary nonlinear material model”, Proc. Appl. Math. Mech. 16, 717-718 (2016) http://onlinelibrary.wiley.com/doi/10.1002/pamm.201610347/pdf
Eschenauer, H.A., Kobelev, V.V., Schumacher, A. (1994): „Bubble method for topology and shape optimization of structures“. Journal of Structural Optimization 8, 42-51.
Eschenauer, H.A., Schumacher, A. (1993): „Possibilities of Applying Various Procedures of Topology Optimization to Components subject to Mechanical Loads“. ZAMM-Z. angew. Math. Mech. 73, T 392-T394.
