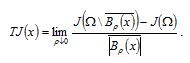Die Idee der Topologischen Ableitung ist es, die Sensitivität des Zielfunktionals bezüglich eines Punktes im Entwurfsraum durch das Einbringen eines Lochs und damit durch direkte Änderung der Topologieklasse zu gewinnen. Die Information, wie sensitiv das Zielfunktional auf das Einbringen eines Lochs an einem Punkt reagiert, kann genutzt werden, um alle Punkte des Entwurfsraums zu bewerten (Bild 1).
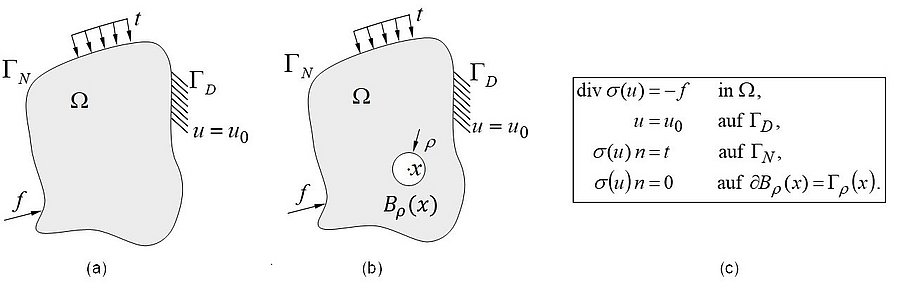
Bild 1: Mechanisches Problem auf dem gesamten Körper, b) mechanischer Körper mit Loch, c) Gleichgewichtsbedingungen
Für das Optimierungsproblem basierend auf dem Funktional J(Ω) und den mechanischen Gleichgewichtsbedingungen kann die Topologische Ableitung ermittelt werden. Hierzu wird in den Entwurfsraum am Punkt x eine Fehlstelle in Form einer Hohlkugel, hier als Bρ(x) bezeichnet, mit Radius ρ eingefügt (vergl. Bilder. So lässt sich der Differenzenquotient schreiben als
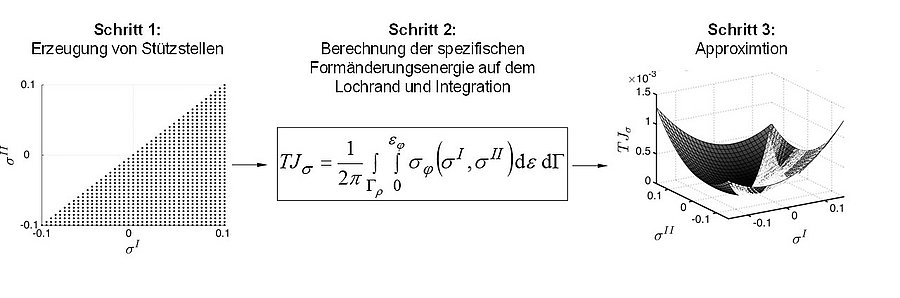
Bild 2: Numerischer Ansatz zum Erstellen einer Approximationsfläche für die Topologische Ableitung
Für lineare Aufgabenstellungen ist die Methode etabliert, für hochgradig nicht-lineare Aufgabenstellung existieren derzeit keine brauchbaren Lösungen. Hier setzt das am Lehrstuhl bearbeitete DFG-Projekt „Topologische Ableitungen zur Topologieoptimierung crashbelasteter Strukturen“ an. Die Topologischen Ableitungen werden numerisch bestimmt und mit analytischen Funktionen in den Optimierungsprozess von Crashstrukturen integriert. Bild 2 zeigt einen numerischer Ansatz zum Erstellen einer Approximationsfläche für die Topologische Ableitung.
Weider, K., Schumacher, A. (2018): "Efficient analysis of topological sensitivities for crash problems using LS-Dyna implicit" appears in the Proceedings of the LS-DYNA Forum 2018, 15.-17.10.2018 in Bamberg
Weider, K., Schumacher, A. (2018): "Adjoint method for Topological Derivatives for optimization tasks with material and geometrical nonlinearities" appears in the Proceedings of the 6th International Conference on Engineering Optimization (EngOpt2018), 17-19 September 2018, Lisboa, Portugal
Weider, K., Schumacher, A. (2018): "A topology optimization scheme for crash loaded structures using Topological Derivatives", in: Schumacher, A., Vietor, T., Fiebig, S., Bletzinger, K.-U., Maute, K. (Hrsg.): Advances in Structural and Multidisciplinary Optimization, Proceedings of the 12th World Congress of Structural and Multidisciplinary Optimization (WCSMO12), Springer Nature, 1601-1614, 2018
Weider, K., Schumacher, A. (2016): “On the calculation of Topological Derivatives considering an exemplary nonlinear material model”, Proc. Appl. Math. Mech. 16, 717-718 (2016) http://onlinelibrary.wiley.com/doi/10.1002/pamm.201610347/pdf
Eschenauer, H.A., Kobelev, V.V., Schumacher, A. (1994): „Bubble method for topology and shape optimization of structures“. Journal of Structural Optimization 8, 42-51.
Eschenauer, H.A., Schumacher, A. (1993): „Possibilities of Applying Various Procedures of Topology Optimization to Components subject to Mechanical Loads“. ZAMM-Z. angew. Math. Mech. 73, T 392-T394.
